Construct Decoding Graph

In this chapter you'll learn how to construct your own decoding graph. Please make sure you understand everything about decoding graph in the Problem Definition Chapter.

You can download the complete code here.

Code Definition

We construct a customized repetition code with non-i.i.d. noise model. That is, each qubit can have different probability of errors. First we define a class representing this customized QEC code. It must have two functions: get_positions and get_initializer. We leave the detailed implementation of them to later part. For the code itself, it takes a code distance \( d \) and a list of error rates \( \{ p_e \} \) specifying the error rate on each of the \( d \) data qubits.

import fusion_blossom as fb
import math

class CustomRepetitionCode:
    """A customize repetition code with non-i.i.d. noise model"""
    def __init__(self, d, p_vec):
        assert len(p_vec) == d
        self.d = d
        self.p_vec = p_vec
    def get_initializer(self):
        # missing implementation
    def get_positions(self):
        # missing implementation

Construct Initializer

There are \( d \) qubits in a chain, and the repetition code stabilizers exist in between every neighbor pair of qubits. Thus, there are \( d-1 \) stabilizer qubits. For simplicity we assume there are no measurement errors so we just need to decode a single round of measurement, which has \( d-1 \) real vertices. Since the qubit on the left and right will generate a single non-trivial measurement event, a virtual vertex is added on the left and right respectively. Thus, there are vertex_num = (d - 1) + 2 vertices in the decoding graph, in which the first and last are virtual vertices.

For the edges, we first calculate the weight using \( w_e = \ln \frac{1 - p_e}{p_e} \). The fusion blossom algorithm takes even integer weight as input (which is also the default and recommended behavior in Blossom V library). In order to minimize numerical error in the computation, we scale all the weight up to a maximum of 2 * max_half_weight.

class CustomRepetitionCode:
    def get_initializer(self, max_half_weight=500):
        vertex_num = (self.d - 1) + 2
        virtual_vertices = [0, vertex_num - 1]
        real_weights = [math.log((1 - pe) / pe, math.e) for pe in self.p_vec]
        scale = max_half_weight / max(real_weights)
        half_weights = [round(we * scale) for we in real_weights]
        weighted_edges = [(i, i+1, 2 * half_weights[i]) for i in range(vertex_num-1)]
        return fb.SolverInitializer(vertex_num, weighted_edges, virtual_vertices)

An example output for d = 7, p_vec = [1e-3, 0.01, 0.01, 0.01, 0.01, 1e-3, 1e-3] is

SolverInitializer {
    vertex_num: 8,
    weighted_edges: [(0, 1, 1000), (1, 2, 666), (2, 3, 666), (3, 4, 666)
        , (4, 5, 666), (5, 6, 1000), (6, 7, 1000)],
    virtual_vertices: [0, 7]
}

Construct Positions [Optional]

Positions are required only when you want to use the visualization tool. We just put all the vertices in a row in a equal space, although the actual weight of edges might be different.

class CustomRepetitionCode:
    def get_positions(self):
        return [fb.VisualizePosition(0, i, 0) for i in range(self.d + 1)]

Code Initialization

p_vec = [1e-3, 0.01, 0.01, 0.01, 0.01, 1e-3, 1e-3]
code = CustomRepetitionCode(d=len(p_vec), p_vec=p_vec)

Construct Syndrome

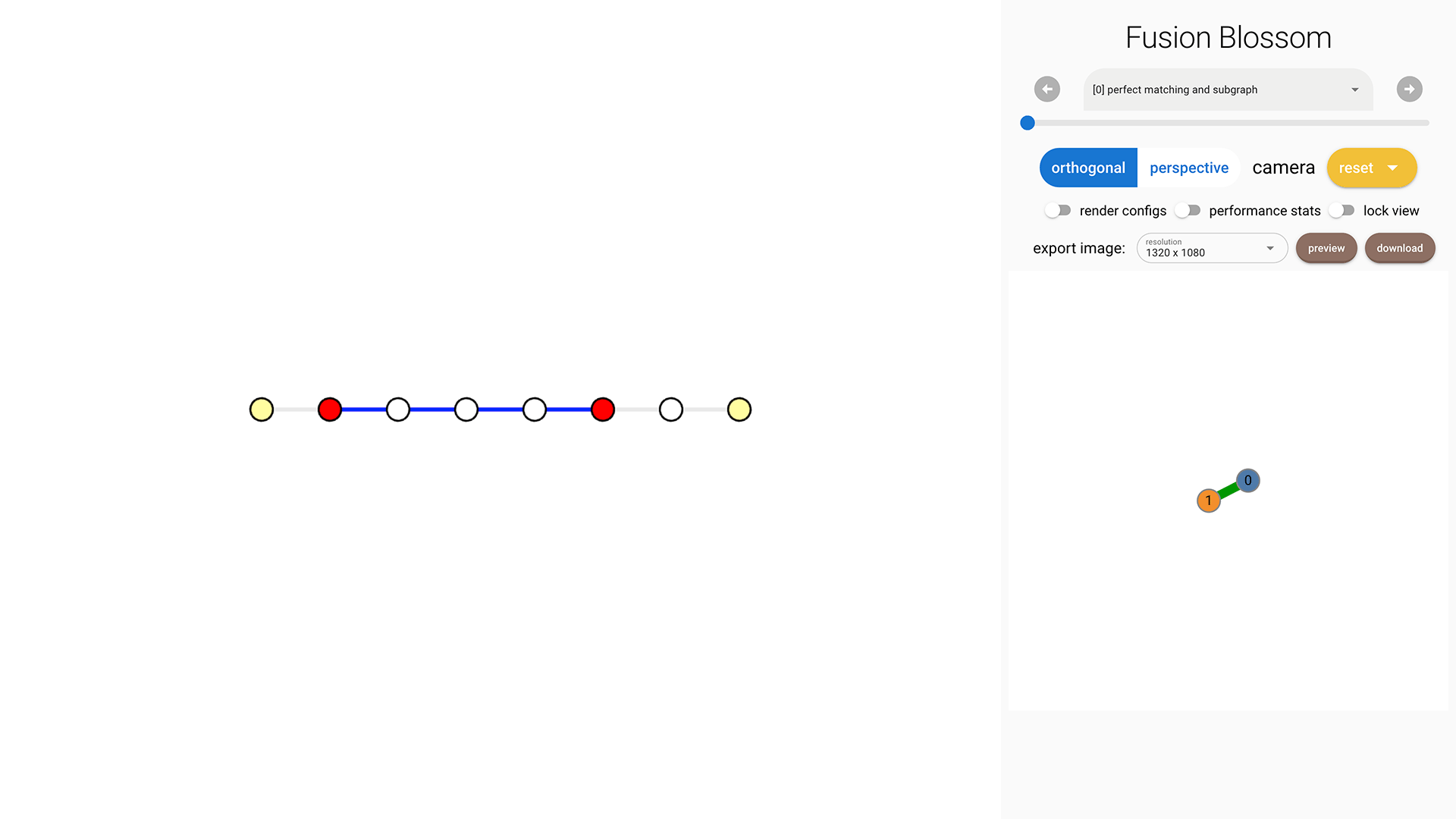
We use a syndrome pattern below to demonstrate the effect of weights.

syndrome = fb.SyndromePattern(defect_vertices=[1,5])

As shown in the following image, there are 4 edges selected in the Minimum-Weight Parity Subgraph (MWPS). This is because the weight sum of these 4 edges is 2664 but the sum of the other 3 complementary edges is 3000. This can also be explained by the fact that the probability is roughly \( 0.01^4 = 10^{-8} \) for the MWPS, but the complementary parity subgraph has a probability of roughly \( 0.001^3 = 10^{-9} \) which is less likely.

Visualize Result

The same process as in Example QEC Codes Chapter.

visualizer = None
if True:  # change to False to disable visualizer for faster decoding
    visualize_filename = fb.static_visualize_data_filename()
    positions = code.get_positions()
    visualizer = fb.Visualizer(filepath=visualize_filename, positions=positions)

initializer = code.get_initializer()
solver = fb.SolverSerial(initializer)

solver.solve(syndrome)

subgraph = solver.subgraph(visualizer)
print(f"Minimum Weight Parity Subgraph (MWPS): {subgraph}")  # Vec<EdgeIndex>

if visualizer is not None:
    fb.print_visualize_link(filename=visualize_filename)
    fb.helper.open_visualizer(visualize_filename, open_browser=True)

Fusion Blossom Tutorial